Foundations of Mutation Analysis
This is an expansion on the implications of our recent publication on the Competent Programmer Hypothesis.
A few definitions: A mistake is a problem in the logical conceptualization of the program in the programmers mind. A fault is a lexical problem within a program, which can lead to compilation error if the compiler catches it, or can lead to incorrect program if the compiler fails to catch it. An error is an incorrect state during the execution of a program which happens due to the execution passing through a fault (for our purposes – there can be other causes of errors). When the error manifests in a detectable deviation in behavior of the program, we call the deviation a failure.
Mutation analysis relies on two fundamental assumptions — The Competent Programmer Hypothesis and The Coupling Effect. The Competent Programmer Hypothesis states that programmers make simple mistakes, such that the new fixed program is not completely different, but within the syntactic neighborhood of the original. The Coupling Effect states that if a test case is able to identify faults in isolation, it will overwhelmingly be able to identify it even in the presence of other faults.
For some intuition about what this means, consider a perfect program as a perfect sphere (Fig.1).
Fig.1 A perfect program.
Any bugs (faults) that cause a failure in this program can be represented as a dimple in the sphere surface, as we see in (Fig.2).
Fig.2 A program with a simple fault.
It can be found by an appropriate test case that checks for imperfection at that point. Of course, in real world, the situation is more complex, with multiple faults (Fig.3)
Fig.3 A program with multiple faults.
Remember that a test suite is a specification for the behavior of a system. The question that mutation analysis seeks to answer is, how closely do the tests specify behavior of the system. For this, we start with the assumption (irrespective of the actual condition) that the program as it is written is the correct one. The question is how much variation of this program is permitted by the test suite. The more variation a test suite permits, the worse it is, as a specification.
The percentage of mutants that is thus detected is taken as a measure of the effectiveness of the test suite in question (in that the specification allows only that much room for variation).
So, now we can see why we need the Competent Programmer Hypothesis. We need it because we are trying to determine how many variants of the program within the syntactic neighborhood is allowed, and CPH allows us to discount the programs that are lexically distant. The Coupling Effect is necessary because it specifies the outcome of interactions. For example, when two faults interact such as in (Fig.4)
Fig.4 Interacting faults.
it can result in a range of results. For example, the resulting failure can become easier to find, and trigger the test cases for both constituent faults (Fig.5).
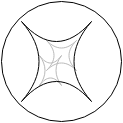
Fig.5 Complex fault with a larger semantic footprint.
Similarly, the faults may even interact with each other, curtailing the propagation of error, such that the final failure is only detectable by a subset of test cases that were able to detect the constituent faults (Fig.6).
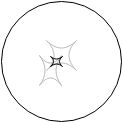
Fig.6 Complex fault with a smaller semantic footprint.
The Coupling Effect suggests that the former is more probable than the later. That is, the complex faults are generally more easier to detect than simple faults.
However, we can immediately see that there are multiple problems with this definition. The first is the question of syntactic neighborhood. What exactly is a simple fault?, and what is a complex fault? Secondly, how do we incorporate features in this definition? Remember that the dividing line between features and bugs change as the levels of abstraction change. For example, an unimplemented, stubbed sort function is a missing feature at the function level. However, if it is relied on by another class, it becomes a bug.
Traditional mutation analysis defines the syntactic neighborhood as within a single token distance. That is, simple faults are faults that are caused by changes in single tokens, while higher order faults are caused by multiple tokens. The problem with this definition is that, this formulation of simple faults do not seem to emulate the real world faults. Our research shows that real world faults are more complex, and we need to take into account at least 10 tokens to account for at least 90% of the faults. This makes the lexical neighborhood as large as expressions and lines, or even functions (not just single tokens, which are often as low as 30%). Further, there is also the problem of mutation operators such as statement and expression deletion, which by the current definition is a complex fault, but intuitively feels like a simple fault (a fault that is caused by a programmer forgetting to add a line).
This suggests a need to re-examine our initial definitions. We suggest the definition of a simple fault should be changed to A simple fault is a fault that can be corrected by changes to a single lexical unit. This ties the definition of a simple fault to a lexical unit under consideration. The lexical unit in question should be identified by statistical analysis of bug fixes (to be done in future research). (Note that if one reduces the lexical unit to tokens, we get the traditional definition of simple faults.) Our formulation cleanly resolves the dichotomy between features and fixes, as the features are now just faults in a larger lexical unit. (This is supported by our empirical analysis which suggests that there is little difference between the size of fault fixes and feature additions). Finally, by our definition, a higher order mutant is a mutant that is composed of faults in multiple lexical units.
So, what is next? We need to first find the most useful lexical unit empirically, that can be used to determine the lexical neighborhood for a program. Our initial empirical analysis suggests that it may be expressions, statements, or functions. Next we need to identify mutation operators that can transform these lexical units such as functions correctly to emulate faults.
A number of such operators can be imagined. For example, a simple stubbing operator can emulate feature additions. Removing or rearranging synchronization primitives such that not all paths are protected can emulate faults in concurrency. Resource allocation mistakes can be emulated similarly with rearranging allocation and deallocation primitives. While this introduces a limited context sensitivity to mutant generation, we gain the ability to incorporate more complex faults as more patterns of faults (such as the heart bleed bug) become known. we can incorporate missing taint checks, or missing exception handling to investigate robustness of test suites against these errors.
One may ask what we gain by considering these as simple faults rather than as higher order faults as it is done traditionally in mutation analysis. The benefit is that our definition of first order can now match the intuitive definition of bugs in the software industry, and higher order mutants are actual interactions between bugs as we understand them (traditionally a blind spot of mutation analysis), rather than just multiple token changes at the same location, that most software practitioners will consider as part of the same bug.
Adopting this definition, and implementing mutation operators that actually resemble real faults can lead to better measurement of the effectiveness of test suites in the real world.